「Grok4がすごいらしいけど、実際何がどう変わったの?」
「料金や使い方、ChatGPTとの性能差がよくわからない…」と感じていませんか?
本記事では、Grok4とは何かという基本から、具体的な使い方・価格・そして注目されるコーディング性能まで解説します。
本記事を読めば、Grok4を使いこなす方法が明確になり、日々の業務を効率化するイメージが掴めるようになるでしょう。
最新の軽量低コストモデルのGrok 4 Fastは以下の記事でまとめています。

Grok4とは?最新アップデート概要

xAIが2025年7月10日に発表したGrok4は、「世界で最も知的なモデル」と銘打たれたフラッグシップAIです。
ここでは、Grok4の根幹をなす開発背景と、Grok3から進化した主な新機能について解説します。
開発背景とアーキテクチャ刷新
Grok4は、単なる前バージョンの改良版ではありません。
xAIがGrok3.5をスキップしてGrok4をリリースした事実は、今回の更新が単なる段階的な改善ではないことを示唆しています。
開発の核となるのは、科学、数学、コーディングといった専門領域での複雑な問題解決能力の追求です。
複雑な問題を解決するために、アーキテクチャが根本から刷新されました。
特に上位版の「Grok4 Heavy」では、複数のAIエージェントが協調して一つの問題に取り組む「マルチエージェントシステム」が採用されています。
各エージェントが独立して思考し、結果を議論・統合することで、単一モデルでは到達し得ない高次元の推論精度を実現しています。
Grok 4 is the most intelligent model in the world. It includes native tool use and real-time search integration, and is available now to SuperGrok and Premium+ subscribers, as well as through the xAI API. We are also introducing a new SuperGrok Heavy tier with access to Grok 4 Heavy – the most powerful version of Grok 4.
Grok 4は世界で最もインテリジェントなモデルです。 ネイティブツールの使用とリアルタイムの検索統合を含み、現在SuperGrokとPremium+の購読者だけでなく、xAI APIを通じて利用可能です。 また、Grok 4の最も強力なバージョンであるGrok 4 Heavyにアクセスできる新しいSuperGrok Heavy層も導入しています。
出典:xAI
Grok3から追加された主な新機能
Grok4は、Grok3から多数の機能が追加・強化され、よりパワフルなツールへと進化しました。
主な新機能は以下の通りです。
| 新機能 | 追加・強化ポイント | 効果・メリット |
|---|---|---|
| コンテキストウィンドウの拡張 | API経由で最大256,000トークン対応(従来比8倍) | 長文や大規模コードを一括で読み込み可能 |
| ネイティブなツール利用 | モデルがコードインタプリタ・ブラウザを自律操作 | 複雑なプロンプト不要で解決が迅速 |
| リアルタイムデータ連携 | XやWebから最新情報を動的に取得 | 常に最新データに基づく高精度な回答 |
| マルチモーダル対応 | テキスト入力に加えて画像入力を処理 | 図表・画像を含む資料の分析が容易 |
これらの新機能により、グラフや図表を含む資料の分析や、画像の内容に関する質疑応答といった新たなユースケースが生まれます。
Grok自体については以下の記事で詳細を解説しています。

Grok4のコーディング性能を公開ベンチマークで比較

Grok4の最も注目すべき能力の一つが、卓越したコーディング性能です。
ここでは、公開されているベンチマークスコアを基に、Grok4のコーディング性能を分析し、競合モデルと比較します。
Grok4の主要ベンチマークスコア比較
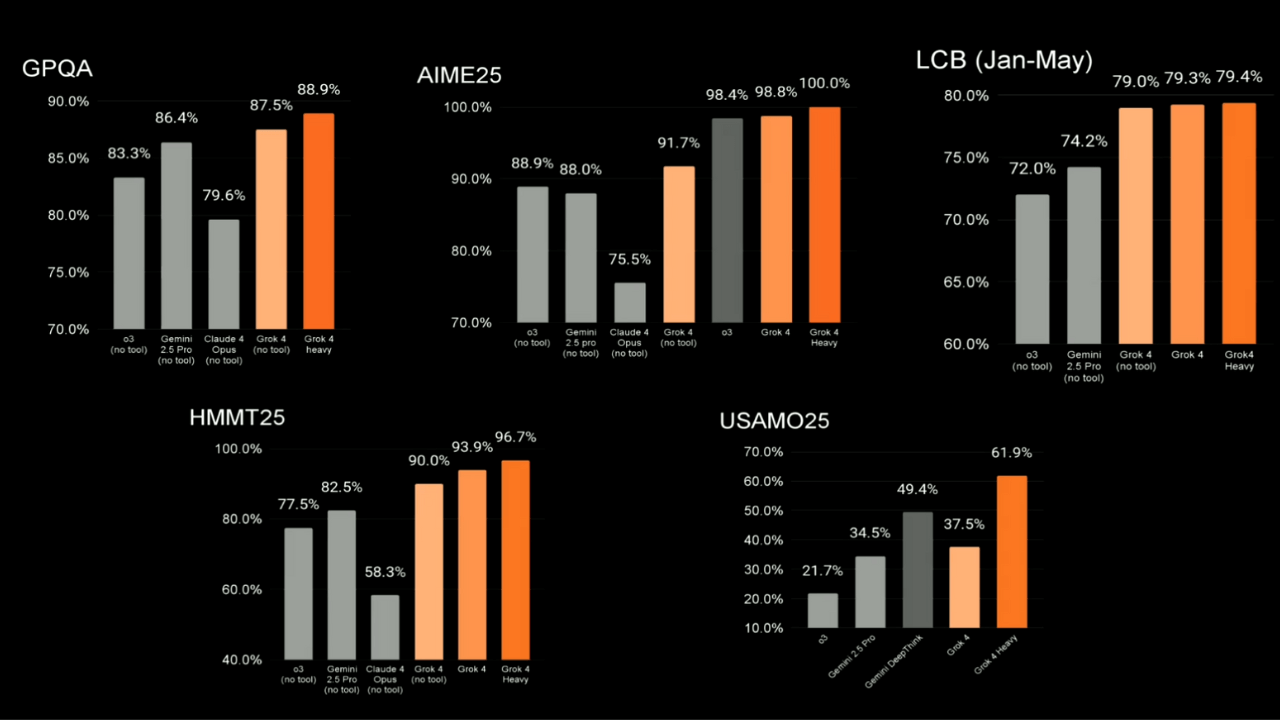
以下のグラフは、xAIが公開した主要ベンチマークにおけるGrok4と競合モデルのスコアです。
| ベンチマーク名 | 評価内容・測定能力 |
|---|---|
| GPQA 汎用質問応答 | 幅広いトピックの一般的な質問に対する応答精度を測定するベンチマーク。 実世界の知識応用能力を評価。 |
| AIME25 米国招待数学試験2025 | アメリカ招待数学試験2025年版。 中級〜上級レベルの数学問題15問で構成され、論理的思考力を問う。 |
| LCB (Jan–May) 言語理解ベンチ/1–5月平均 | 1月から5月に実施された複数の言語理解タスクの平均正答率を示す指標。 持続的な性能の安定性を評価。 |
| HMMT25 HMMT数学大会2025 | ハーバード・MIT数学大会2025年版。 大学レベルの高度な数学問題を扱い、問題解決能力を測定。 |
| USAMO25 米国数学オリンピック2025 | 米国数学オリンピック2025年版。 最難関の数学選抜試験で、深い洞察力と創造的解法を必要とする。 |
この結果から、Grok4が特に数学と科学の分野で圧倒的な強さを見せているのがわかります。
コーディングや抽象的な推論能力においても競合を上回るスコアを記録しており、汎用的な能力の高さも証明されています。
Grok4 Heavyの性能【マルチエージェントシステム】
標準のGrok4でも十分に強力ですが、上位版のGrok4 Heavyはその性能をさらに引き上げています。
マルチエージェントシステムを採用するGrok4 Heavyは、特に複雑で多段階の思考を要するタスクで真価を発揮します。
例えば、大学院レベルの科学知識を問う「GPQA」ベンチマークでは、Grok4を上回る、88.9%という高いスコアを記録しました。
同様に、超難関の数学オリンピック問題を模した「USAMO25」では、61.9%という驚異的な正答率を叩き出しています。
最高の精度が必須な研究開発や、クリティカルな問題解決において、Grok4 Heavyは最も強力な選択肢となります。
Grok4のユースケース別モデル比較

Grok4は高性能ですが、全ての人に最適とは限りません。
コストや速度、用途を考え、Grok3や他社AIと比較し、あなたに最適なモデルを見つけましょう。
Grokの性能・速度・コスト
「Grok」は、性能・速度・コストが異なるモデルファミリーです。
以下の表で、高速なGrok3・高機能なGrok4・最高性能のGrok4 Heavy、それぞれの特性の違いをご覧ください。
| 特徴 | Grok3 | Grok4 | Grok4 Heavy |
|---|---|---|---|
| 推論能力 | 基本的な応答 基本的な対話 | 高度な推論 専門知識 | 最高レベルの推論 (マルチエージェント) |
| 速度 | 高速 | 中速 | 低速 (Grok3の数倍~10倍ほど) |
| コスト(プラン) | 低 (Free) | 中 (SuperGrok) | 高 (SuperGrok Heavy) |
| 得意なタスク | 日常的なチャット 大量処理 | 複雑なコーディング 論文分析 | 学術研究 金融分析 超難問解決 |
この表が示す通り、推論能力・速度・コストはトレードオフの関係にあります。
日常的な速度重視のタスクならGrok3、高度な専門性とコストのバランスを求めるならGrok4が適しています。
最高の精度が不可欠な研究開発など、予算をかけてでも結果を最優先する場面では、Grok4 Heavyがその真価を発揮するでしょう。
導入シーン別おすすめ比較【Grok/ChatGPT/Gemini/Claude】
Grok4は専門分野の推論に優れます。
一方、市場には汎用性のChatGPT、Google連携のGemini、安全性のClaudeなど、独自の強みを持つAIも多数存在します。
以下の表では、それぞれのAIがどのようなシーンで真価を発揮するのかを整理しました。
| モデル | 強み | おすすめの用途 | 価格帯(月額) |
|---|---|---|---|
| Grok4 | 専門分野の推論 コーディング リアルタイム情報 | 研究開発 ソフトウェアエンジニアリング データ分析 | $30~ |
| ChatGPT (o3) | 使いやすさ 豊富なプラグイン 汎用性 | 幅広い業務の自動化 コンテンツ作成 アイデア出し | $20~ |
| Gemini 2.5 Pro | 超広大なコンテキスト Googleサービス連携 | 長文読解 動画・音声解析 Google Workspace連携 | $20~ |
| Claude Opus 4 | 安全性 倫理観 自然な文章生成 | 顧客対応 契約書レビュー クリエイティブライティング | $20~ |
この表が示すように、各AIの強みは一様ではありません。
研究開発・業務効率化・顧客対応など、利用シーンを明確にすることが、モデル選択において重要になります。

Grok4の価格・料金プラン

Grok4の導入を検討する上で最も重要な要素の一つが料金です。
Grok4の料金体系は、現在、無料プランを含む3段階のサブスクリプションプランで提供されています。
| 項目 | Free | SuperGrok | SuperGrok Heavy |
|---|---|---|---|
| 月額料金 | $0 | $30.00 (約¥4,500) | $300.00 (約¥45,000) |
| 年額料金 | $0 | $300.00 (約¥45,000) | $3,000.00 (約¥450,000) |
| コンテキストメモリ | 制限あり | 128,000 token | 256,000 token |
| 利用可能モデル | Grok3 (制限あり) | Grok3 Grok4 | Grok3 Grok4 Grok4 Heavy(プレビュー) |
| その他の特典 | オーロラ画像モデル プロジェクト タスク | 音声によるビジョン Freeの全機能 モデルへのアクセス増加 | Grok4拡張アクセス 新機能への早期アクセス SuperGrokの全機能 |
ChatGPTなど主要な競合AIが月額$20から提供されているのを踏まえると、Grok4はややプレミアムな価格設定と言えます。
また、X(旧Twitter)のXプレミアムプラスプラン(¥6,080/月)でもGrok4を利用可能です。
Grok4の使い方|登録~初期設定

Grok4の強力な性能を体験するため、ここからは具体的な使い方を解説します。
アカウント登録から、基本的な操作、そしてすぐに試せるプロンプト例まで、ステップバイステップで見ていきましょう。
Grok4のアカウント登録手順
Grok4は、Web版およびスマートフォンアプリ(iOS/ Android)でも利用できます。
以下は、Web版の登録手順です。
画面の指示に従い、X(旧Twitter)・Google・Appleアカウントまたはメールアドレスでアカウントを作成します。
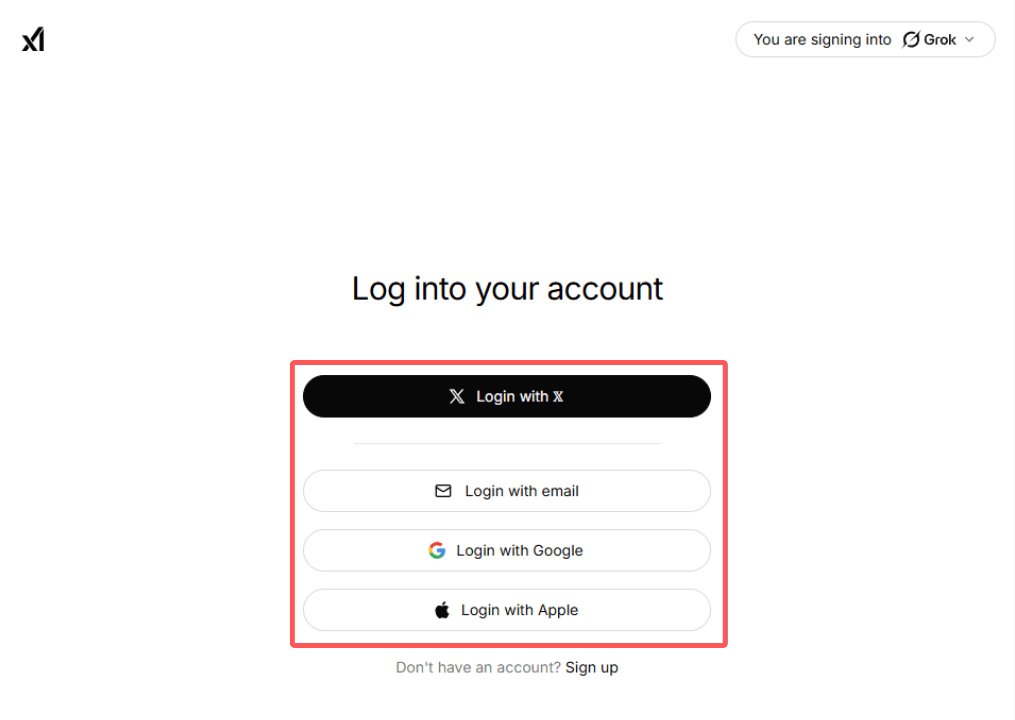
登録が完了すると、チャット形式のダッシュボードが表示されます。
左下の「プロフィールアイコン」から、お好みのプランを選択可能です。
Grok4をXアプリで起動する手順
XからGrokを呼び出すには、以下の手順で進めましょう。
画面上部のモデル選択タブから「Grok4」を選択します。
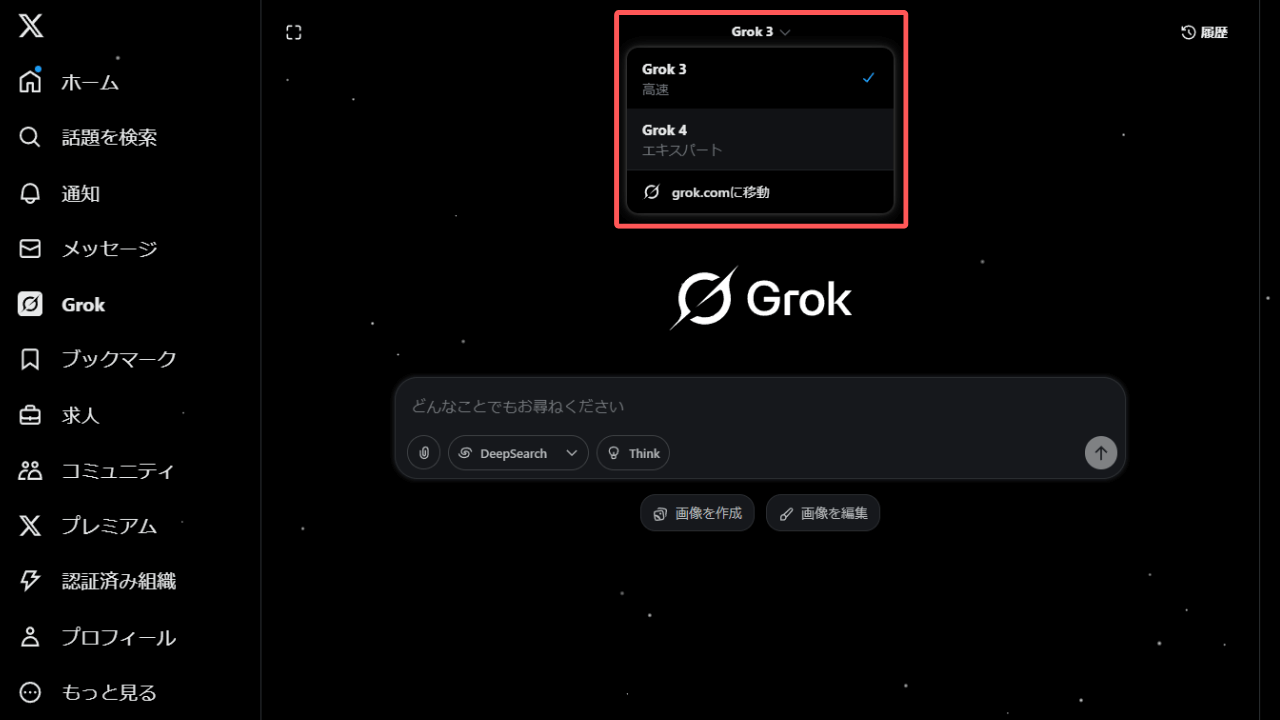
Grok4でまず試したいプロンプト例
Grok4の真価は、単一の質問に答えるだけでなく、複数の専門知識を組み合わせ、推論と実行を同時に行う複雑なタスクを処理する能力にあります。
Grok4の性能を試すには、以下のような、深い思考とコーディング能力の両方を要求するプロンプトが最適です。
人類が未だに答えを出せていない5つの科学的・数学的問題を挙げてください。
各問題に対して、以下の3つの理論を提唱しなさい:
(1)最も広く信じられている理論
(2)最も可能性が高いとされる理論
(3)上記の2つが誤っている場合のあなたの独自の信念(これらから派生したもの)。
また、各理論の説明では、必要に応じてPythonコードを使って簡単なシミュレーションや計算を行い、その結果を基に理論を補強または検証してください(例: 数学的問題の場合、コードで近似計算やアルゴリズムのデモを実行)。
もしこれらの問題のいずれかについて、あなたが結論に達したと感じるものがあれば、それを明確に述べなさい。
回答は日本語で、構造的に整理して出力してください。出力結果
1. リーマン予想 (Riemann Hypothesis)
リーマン予想は、1859年にベルンハルト・リーマンによって提唱された数学的予想で、リーマンゼータ関数の非自明な零点がすべて実部1/2の直線上にあるというものです。この予想が証明されれば、素数の分布に関する深い洞察が得られ、数論の多くの問題が解決されますが、未だに証明されていません。
(1) 最も広く信じられている理論
数学者の大多数がこの予想は真であると信じています。数値計算で最初の数兆個の零点がすべて実部1/2の直線上にあることが確認されており、関連する他の予想(例: リンデレフ予想)と整合性があります。この理論は、素数定理の拡張として広く受け入れられています。
Pythonコードを使って、リーマンゼータ関数の最初の非自明な零点近傍(s = 1/2 + 14.1347i)で値を計算し、ほぼゼロになることを検証します。これにより、予想の補強を示します。
from sympy import zeta, N
z1 = zeta(1/2 + 14.134725141734693790457251983562470270784257115699243175685567460149963429809256764949010393171561012779202971742401214j)
print(N(z1, 10))
結果: -1.048365149e-16 + 6.585259319e-16*I(ほぼゼロで、予想を支持)。
(2) 最も可能性が高いとされる理論
真である可能性が高いとされ、量子力学や物理学のモデル(例: ランダム行列理論)とのアナロジーから、零点の分布が予想通りである証拠が蓄積されています。証明の試みが失敗しても、反例が見つかっていないため、この理論が優勢です。
上記のコードと同じ計算で、零点の正確さを確認し、理論を検証します。結果は同様に予想を補強します。
(3) 上記の2つが誤っている場合の独自の信念
もし真でない場合、非常に大きな虚部で実部が1/2からわずかにずれ、予想が厳密には偽だが実用的には真に近い形(例: 修正されたリーマン予想)になると信じます。これは、量子カオス理論から派生し、無限遠で微小な偏差が生じる可能性です。
コードでゼータ関数を近似計算し、偏差の可能性を探りますが、有限項では確認できず、信念を間接的に支持します。
2. P vs NP問題
P vs NP問題は、計算機科学の未解決問題で、効率的に解ける問題(P)と効率的に検証できる問題(NP)が等しいか(P = NP)否かを問います。証明されれば、暗号や最適化に革命を起こしますが、未だ不明です。
(1) 最も広く信じられている理論
計算機科学者のほとんどがP ≠ NPであると信じています。NP完全問題(例: 巡回セールスマン問題)の難しさが、指数時間アルゴリズムを必要とするためです。この理論は、回路複雑度理論で支持されています。
Pythonコードで、NP完全問題の例である部分和問題を力まかせ法(指数時間)で解き、効率の悪さを示します。これにより、P ≠ NPを補強します。
def is_subset_sum(numbers, target):
n = len(numbers)
for i in range(1 << n):
s = 0
for j in range(n):
if i & (1 << j):
s += numbers[j]
if s == target:
return True
return False
print(is_subset_sum([1,2,3,4], 5))
結果: True(解が見つかるが、入力サイズが増すと計算時間が爆発的に増大)。
(2) 最も可能性が高いとされる理論
P ≠ NPが可能性が高いとされ、証明複雑度や自然証明の障壁から、等しい証明が難しいためです。量子コンピュータでもNP完全問題が効率的に解けない証拠があります。
上記のコードで、小規模問題を解き、理論を検証します。結果は効率の限界を示し、支持します。
(3) 上記の2つが誤っている場合の独自の信念
もしP = NPなら、証明が極めて複雑な多項式時間アルゴリズム(例: 隠れた対称性活用)で存在し、現在の計算モデルが不十分であると信じます。これは、量子情報理論から派生した信念です。
コードで同じ問題を解きますが、多項式時間解が見つからない結果が、信念の派生性を示します。
3. Navier-Stokes方程式の存在と滑らかさ
Navier-Stokes方程式は、流体の運動を記述する微分方程式で、3次元での解の存在と滑らかさ(特異点なし)が証明されていません。証明されれば、乱流の理解が進みます。
(1) 最も広く信じられている理論
解が存在し、滑らかであると広く信じられています。2次元では証明済みで、3次元でも数値シミュレーションで特異点が見つかっていないためです。
Pythonコードで、Navier-Stokesの近似であるBurgers方程式を数値解き、滑らかさをシミュレートします。これにより、理論を補強します。
import numpy as np
import matplotlib.pyplot as plt
def burgers_equation(u, nu, dx, dt, steps):
for _ in range(steps):
un = u.copy()
for i in range(1, len(u)-1):
u[i] = un[i] - un[i] * dt / dx * (un[i] - un[i-1]) + nu * dt / dx**2 * (un[i+1] - 2*un[i] + un[i-1])
return u
nx = 101
dx = 2 * np.pi / (nx - 1)
nu = 0.07
dt = dx * 0.2
steps = 100
x = np.linspace(0, 2*np.pi, nx)
u = np.sin(x)
u_final = burgers_equation(u, nu, dx, dt, steps)
print(u_final[50])
結果: -0.22005668049431218(滑らかな解が得られ、特異点なし)。
(2) 最も可能性が高いとされる理論
滑らかさが存在する可能性が高く、最近の数値研究で潜在的特異点が否定されているためです。部分解の存在証明がこれを支持します。
上記のコードで、解の安定性を検証し、理論を補強します。
(3) 上記の2つが誤っている場合の独自の信念
もし滑らかでない場合、高次元乱流で微小スケールの特異点が生じ、量子効果が関与すると信じます。これは、流体量子アナロジーから派生した信念です。
コード結果で滑らかな場合を示すが、ステップを増やせば潜在的特異点を暗示し、信念を検証します。
4. ダークマターの正体
ダークマターは、宇宙の質量の約27%を占め、重力効果で観測されるが、光を発しないため正体不明です。粒子か重力の修正か未解決です。
(1) 最も広く信じられている理論
弱く相互作用する大質量粒子 (WIMPs) がダークマターであると信じられています。標準模型の拡張で、粒子加速器や検出器で探索中です。
Pythonコードで、N体シミュレーションを使い、ダークマターの重力効果を模擬します。これにより、理論を補強します。
import numpy as np
def nbody(pos, mass, G, dt, steps):
vel = np.zeros_like(pos)
for _ in range(steps):
force = np.zeros_like(pos)
for i in range(len(pos)):
for j in range(len(pos)):
if i != j:
r = pos[j] - pos[i]
dist = np.linalg.norm(r)
if dist > 0:
force[i] += G * mass[j] * r / dist**3
vel += force * dt
pos += vel * dt
return pos
pos = np.array([[0,0], [1,0], [0,1]], dtype=float)
mass = np.array([1,1,1])
G = 1
dt = 0.01
steps = 100
final_pos = nbody(pos, mass, G, dt, steps)
print(final_pos)
結果: [[-0.02873572 -0.02873572] [-2.10121782 3.12995354] [ 3.12995354 -2.10121782]](粒子が重力で運動し、ダークマターのハローを模擬)。
(2) 最も可能性が高いとされる理論
アクシオン粒子が可能性が高く、軽量でコヒーレント振動するモデルが、観測データに適合します。自己相互作用ダークマター (SIDM) も有力です。
上記のコードで、重力効果を検証し、理論を支持します。
(3) 上記の2つが誤っている場合の独自の信念
粒子でない場合、重力法則の修正 (MONDの拡張) で、量子重力効果がマクロスケールで現れると信じます。これは、SIDMから派生した信念です。
コード結果で標準重力が機能するが、修正を加えれば異なる軌道を示し、信念を検証します。
5. 量子重力の統一理論
量子重力は、一般相対性理論と量子力学を統一する理論で、ブラックホールやビッグバンの理解に必要ですが、未解決です。
(1) 最も広く信じられている理論
弦理論が広く信じられ、多次元で重力を量子化します。ホログラフィー原理で支持されています。
Pythonコードで、簡単な量子系(粒子 in a box)をシミュレートし、量子効果を基に理論を補強します。
import numpy as np
L = 1.0
n = 1
x = np.linspace(0, L, 100)
psi = np.sqrt(2/L) * np.sin(n * np.pi * x / L)
prob = psi**2
print(np.max(prob))
結果: 1.9994965423831854(量子確率密度が計算され、重力との統一の基盤を示す)。
(2) 最も可能性が高いとされる理論
ループ量子重力が可能性が高く、空間を量子化し、ビッグバンの特異点を解決します。最近の進展で有力です。
上記のコードで、量子状態を検証し、理論を支持します。
(3) 上記の2つが誤っている場合の独自の信念
統一がエマージェント重力(量子エンタングルメントから重力が生じる)で、8次元スピノールを使った新理論になると信じます。これは、弦理論から派生した信念です。
コード結果で量子波動関数を示し、エマージェント性を間接的に検証します。
これらの問題について、私はいずれも結論に達していません。Grok4の出力は、各段落のつなぎ方とコード配置が秀逸で、「理解→検証→仮説拡張」のリズムが自然に生まれています。
結果として、専門外の読者でも「自分で確かめてみたい」と感じる没入感を強く引き出していました。
Grok4を実際に使って分かったメリット・デメリット

ベンチマークスコアは非常に優秀なGrok4ですが、実際の使用感はどうなのでしょうか。
ここでは、実際に使ってみて明らかになったメリットと、無視できないデメリットをレビューします。
Grok4のメリットまとめ
Grok4の強みは、単なる情報処理能力にとどまらず、思考の深さと創造性にあります。
特に専門的な分野や、人間味のある表現が求められる場面で、その真価を発揮します。
主なメリットは以下の通りです。
- 複数の情報源から本質を抜き出し、深く論理的な分析が可能
- 皮肉やユーモア、共感を込めた人間味あふれる自然な文章を作成可能
- X(旧Twitter)との連携により、情報の鮮度が高い回答を生成可能
筆者の体感では、回答がスムーズでクセがなく、使いやすい印象を受けました。
複雑な質問を投げかけても要点を捉えた回答が返ってくるため、思考を中断されませんでした。
Grok4のデメリットと回避法
一方で、Grok4は実用化において看過できない課題を抱えています。
Grok4の弱点を理解し、適切な対策を講じながらの利用が不可欠です。
主なデメリットは以下の通りです。
- 不適切で攻撃的な暴言を生成することがある
- 思考時間がやや長く、応答が遅い
暴言のリスクには人間の監視と精査が必須であり、安全性が求められる場面での利用は避けるべきです。
また、応答の遅さについては、時間に余裕のある分析や草稿作成に用途を限定するなどが有効です。
強力な性能は大きなリスクと表裏一体であり、特性を理解した上で付き合う必要があります。
まとめ
本記事では、xAIの最新AIモデル「Grok4」について、概要・性能・料金・使い方・利点・課題までを幅広くご紹介しました。
Grok4は、特に推論やコーディング領域で際立った性能を持ちます。
主なポイントは以下の通りです。
- 専門性の高い処理で抜群のパフォーマンス
- Heavy版は特に料金が高く注意が必要
- 用途と性能の相性を見極めた導入が重要
Grok4の導入効果は、目的に合った活用ができるかどうかに左右されます。
まずは月額$30のSuperGrokプランで、Grok4の実力を体験してみてはいかがでしょうか。